Information Conservation and the Unitarity of Quantum Mechanics
In his book ¡°Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics,¡± Prof. Leonard Susskind explains that information is always conserved according to the basic principle of quantum mechanics, and argues that Hawking was wrong in claiming that information is lost when an object falls into black hole. In more technical terms, information conservation is related to the unitarity of quantum mechanics. In this article, I will explain what unitarity is and how it¡¯s related to information conservation.
A
unitary matrix, U, is a matrix that satisfies 
. In other words, a matrix whose inverse is its Hermitian
conjugate is a unitary matrix. Unitarity of quantum
mechanics means that the time evolution matrix is unitary. Now, let me give you
two examples of the time evolution matrix.
In this example imagine that there are 5 types of possible universes. Of course, there are many more, but the assumption is made for simplicity. After all, the purpose of this article is not to give a complete picture, but rather to explain the key concepts. Let¡¯s label ith universe by (i). So, we have 5 universes, namely:
(1), (2), (3), (4), (5)
Then, physics calculations will predict which universe the initial universe will transform into at every second given what type of universe we had started on. Let¡¯s say for example,
SCENARIO I, RULE I
(1) will transform into (3)
(2) will transform into (1)
(3) will transform into (5)
(4) will transform into (2)
(5) will transform into (4)
So, if our universe is (1), after a second it will become (3), after another second it will become (5) and so on. Notice that in this scenario the information is conserved. i.e. Given the present state of our universe, we can know what the universe was 1 second ago. For example, if universe is (2) now, it must have been (4) 1 second ago.
As we have an example of an information preserving universe, let¡¯s give an example of information non-conserving universe.
SCENARIO II, RULE I
(1) will transform into (3)
(2) will transform into (1)
(3) will transform into (5)
(4) will transform into (3)
(5) will transform into (4)
Could we know what the universe was a second ago, given the present state of the universe?
Let¡¯s check:
SCENARIO II, RULE II
The universe a second before the universe (1) is (2).
The universe a second before the universe (2) is none.
The universe a second before the universe (3) is either (1) or (4).
The universe a second before the universe (4) is (5).
The universe a second before the universe (5) is (3).
This scenario is certainly information non-conserving, since if the universe is (3) now, we don¡¯t know whether the universe was (1) or (4) a second ago.
So far I have explained what information conservation means. Now, I will explain how one can express this in mathematical language.
Let¡¯s denote A_ji=1 if the ith universe transforms into jth universe every second, and zero otherwise.
In the first scenario, we have A_31=A_12=A_53=A_24=A_45=1
In matrix, this can be expressed as follows:
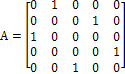
Then, we can certainly express the evolution of the universe as a matrix. Let the first universe, the second universe, the third universe, the fourth universe and the fifth universe be expressed in following ways.
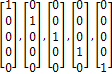
Then, we can express the evolution of the second universe to the first universe as follows.
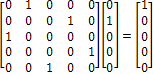
Then,
given these evolution rules dictated by the matrix A and a certain present state
of the universe, what would be the matrix that tells you the universe one
second ago? This should be the inverse matrix of A. However, it¡¯s easy to see that
this matrix is also the Hermitian conjugate of A, if
the inverse matrix exists. If ith universe evolves
into jth universe every second, the jth universe a second ago must be ith
universe. Therefore if 
, then 
. Explicitly,
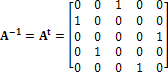
In words, it means the following:
SCENARIO I, RULE II
The universe a second before the universe (1) is (2).
The universe a second before the universe (2) is (4).
The universe a second before the universe (3) is (1)
The universe a second before the universe (4) is (5).
The universe a second before the universe (5) is (3).
For example, the fact that the universe (5) was (3) a second ago can be expressed as follows:
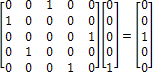
Moreover, needless to say, the universe now is the universe one second after the universe one second ago before now. Explicitly, we can combine ¡°SCENARIO I, RULE I¡± with ¡°SCENARIO I, RULE II¡± as follows.
The universe a second before the universe (1) is (2). (2) transforms back to (1) after a second.
The universe a second before the universe (2) is (4). (4) transforms back to (2) after a second.
The universe a second before the universe (3) is (1). (1) transforms back to (3) after a second.
The universe a second before the universe (4) is (5). (5) transforms back to (4) after a second.
The universe a second before the universe (5) is (3). (3) transforms back to (5) after a second.
Mathematically, this can be expressed as follows:
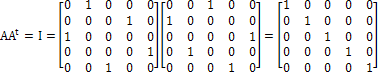
So, we get an identity matrix. Similarly, the universe now is the universe one second before the universe one second from now. Again, we can explicitly combine ¡°CASE I, RULE I¡± with ¡°SCENARIO I, RULE II¡± as follows.
(1) transforms to (3) after a second. The universe a second before the universe (3) is (1).
(2) transforms to (1) after a second. The universe a second before the universe (1) is (2).
(3) transforms to (5) after a second. The universe a second before the universe (5) is (3).
(4) transforms to (2) after a second. The universe a second before the universe (2) is (4).
(5) transforms to (4) after a second. The universe a second before the universe (4) is (5).
It can be expressed as follows.
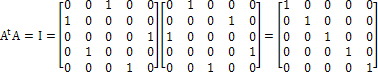
So far so good.
However,
the identity 
only holds for
information conserving cases. If information is not conserved, such as in our
second scenario, this identity doesn¡¯t hold. This is because we cannot know
which universe it was if our universe is (3) now. In other words, we see that
neither 
nor 
is identity matrix. Let¡¯s
explicitly check this for our second scenario.
Combining SCENARIO II, RULE I and RULE II, we have:
The universe a second before the universe (1) is (2). (2) transforms back to (1) after a second.
The universe a second before the universe (2) is none.
The universe a second before the universe (3) is either (1) or (4). (1) and (4) transforms back to (3) after a second.
The universe a second before the universe (4) is (5). (5) transforms back to (4) after a second.
The universe a second before the universe (5) is (3). (3) transforms back to (5) after a second.
So (1) comes back to (1). (2) goes to none. (3) comes back to (3) by two routes. (4) goes to (4). (5) goes to (5).
Mathematically, this can be represented as follows:
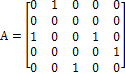
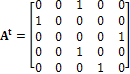
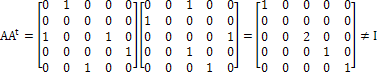
Notice that the remark just mentioned before the above formula implies:
=1,
=0
=2
=1
=1
Similarly, combining SCENARIO I, RULE I with RULE II, we get:
(1) transforms to (3) after a second. The universe a second before the universe (3) is (1) or (4).
(2) transforms to (1) after a second. The universe a second before the universe (1) is (2).
(3) transforms to (5) after a second. The universe a second before the universe (5) is (3).
(4) transforms to (3) after a second. The universe a second before the universe (2) is (4) or (1).
(5) transforms to (4) after a second. The universe a second before the universe (4) is (5).
This implies:
=(
=1
=1
=1
=
=1
=1
Mathematically:
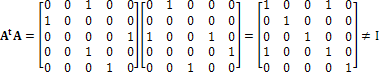
I hope that this article has provided some sense of the reason why the information conservation necessarily implies that the evolution matrix is unitary, or, at least the reason why the information non-conservation necessarily implies that the evolution matrix is non-unitary. Later in the article ¡°A short introduction to quantum mechanics VII: the Unitarity of the time evolution operator,¡± I will interpret the unitarity of time evolution operator as the requirement that the total probability sums up to be 1.