These articles are written with diverse types of audiences in mind, including ordinary high school students, laymen, students learning high school physics, students learning calculus, mathematically oriented high school students, science and engineering students, and physics majors. However, I tried to write these articles as self-contained as possible so that those articles targeted for higher-level readers can be understood if lower-level readers read their prerequisites, which are presented among my articles as well. Also, I have tried to present these articles in a suggested order of reading. Nevertheless, you may want to skip some articles and jump ahead to more interesting ones, unless the articles you skip are prerequisites to those. Of course, if you are a high-level reader, you may not want to read the articles that examine topics which you are already familiar with. In any case, prerequisites are stated in the comments for the grouped articles.
Not every reader will have the same expectation from these articles. Some may want to have just fun and appreciate how beautiful our nature is, while others may be serious and want to become physicists so that they can further find the beauty of nature by themselves. To do so, you have to first know the old, explored territories very well. For these future physicists, I have set three goals in these articles, i.e., three grand subjects that are already explored: Loop quantum gravity, Verlinde gravity and Cosmic Microwave Background anisotropies.
Some may just want to reach one or two of these subjects, while others may want to learn all of them. It’s your choice. However, all of these three grand subjects require prerequisites, which I now turn to explain. See the figure below.
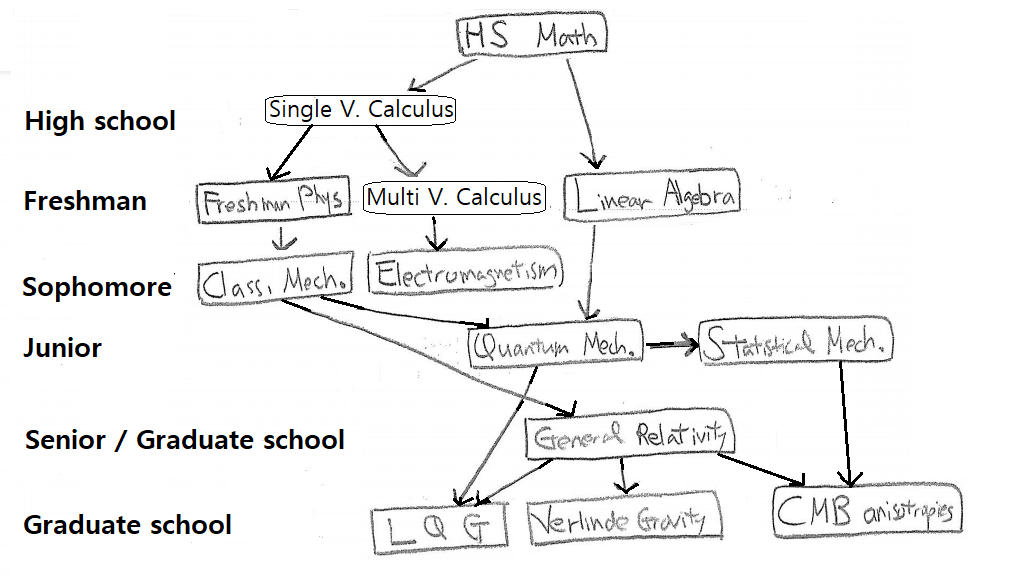
If you plan to study science or engineering in university, you must first study “high school math.” I initially didn’t write articles on it, but I added them to make this webpage as self-contained and accessible as possible. After all, even though most South Korean adults know quite a bit of basic math, many American adults don’t.
Once you know high school math, you need to study “calculus” thoroughly. Many South Korean high school students and advanced American high school students learn “single variable calculus.” Then, if they enter university to major in science or engineering, they learn “multi-variable calculus” in freshman year. We will examine both “single variable calculus” and “multi-variable calculus” closely, as they are to physics, what English language is to Shakespeare’s. Besides “multi-variable calculus,” you are usually required to study “freshman physics” and “linear algebra” in freshman year of college if you intend to major in science or engineering.
A freshman physics course for science and engineering students covers a little bit of classical mechanics, a little bit of thermodynamics, a little bit of electricity and magnetism, a little bit of optics, and a little bit of modern physics (i.e., quantum mechanics and some miscellaneous topics), and a little bit of special relativity. In particular, it doesn’t assume any knowledge of high school physics. I cover the very basic classical mechanics in “Basic high school physics without calculus” and the thermodynamics part in “Entropy” and “Thermodynamics.” I also treated electricity and magnetism in three parts at the high school level, without using any difficult mathematics. However, I completely omit the circuit problems, which are crucial for electrical engineering subjects. I cover the optics part in “Wave.” The modern physics part is covered in “Historical Introduction to Quantum Mechanics.” Special relativity is covered in “Special Relativity” and “Paradoxes in Special Relativity.” Special relativity is very beautiful, and depending on the level, it can be learned either with or without electricity and magnetism. To truly appreciate its beauty, I will teach you special relativity with electricity and magnetism. The first part of “electricity and magnetism” serves as the prerequisite for special relativity.
If you decide to major in physics, your curriculum differs from other science and engineering students, beginning from sophomore year. In sophomore year, you learn “classical mechanics” and “electromagnetism,” and in junior year, you learn “quantum mechanics” and “statistical mechanics.” These four subjects are the key subjects in the physics curriculum. Actually, as I mentioned, you learn each bit of this in freshman physics, but not at the level or depth you will later learn as a physics major. Anyhow, “in theory,” you are supposed to be able to follow these four subjects without having learned freshman physics, as the textbooks you will use do not take off from the material you left off in “freshman physics” but will start all again from the beginning. However, “in practice,” it may not be that easy to follow these four subjects without the knowledge of freshman physics because your professor may not explain in detail the contents already covered in freshman physics, even though these materials are covered in your textbooks. Anyway, if you go to graduate school to study physics, you learn these four subjects once again with more depth and maturity in the first year. Again, “in theory,” you are supposed to be able to follow these four subjects at a graduate level, without having studied them at all at the undergraduate level. But, “in practice,” it is not that easy. Nevertheless, some graduate students are able to follow physics courses successfully at graduate schools without undergraduate degrees in physics, because, as I have just mentioned, the courses begin from the beginning. Anyhow, in senior year, you usually learn a little bit of different branches of physics so that you can get some ideas about what kind of research areas physicists work on. These subjects are not usually mandatory, and I actually took none of them.
Now, let me explain how I present these four key subjects in my articles.
The main thing that sophomore physics majors learn in their classical mechanics courses is how to solve the key equations from classical mechanics for various situations. However, I keep this to a minimum, and present them only mostly in “Mathematical Introduction to Physics.” Instead, I focus more on the basic formalisms (i.e., the derivation and motivation behind the key equations) of classical mechanics, which will turn out to be useful in linking classical mechanics with quantum mechanics.
Physics majors learn electricity and magnetism, which they learned in freshman year, more deeply in their sophomore year, as mentioned earlier. In “Maxwell’s equations,” I will re-visit the three parts of “electricity and magnetism” using multi-variable calculus, culminating in the derivation of Maxwell’s equations. Just like classical mechanics, the main thing sophomore physics majors learn in their electricity and magnetism course is how to solve Maxwell’s equations in various situations. Again, this is something I keep to a minimum, and instead, I focus more on the basic formalisms.
Quantum mechanics, which physics majors usually learn in their junior year, requires the knowledge of calculus and linear algebra learned in their freshman year. In my treatment, I amalgamate a course on basic linear algebra with a course on basic quantum mechanics in one section. In this way, it will give readers more motivation to study linear algebra. They will understand how certain concepts in linear algebra are useful in applications. Besides this mathematical background, quantum mechanics requires some basic physics knowledge, usually taught in a high school or freshman college physics course. However, if you want to understand how quantum mechanics can describe every phenomenon classical physics can describe, you have to learn first the basic formalisms of classical mechanics closely. After presenting the basic quantum mechanics and the basic linear algebra, I will present the connection between classical physics and quantum mechanics, as well as more advanced topics in linear algebra and quantum mechanics.
Statistical mechanics is a huge subject that junior physics majors usually learn after learning the first semester of quantum mechanics. While its details are relatively less important in loop quantum gravity or theoretical particle physics than in cosmology or other branches of physics, its key basic concepts are crucial in understanding the black hole thermodynamics and discovering Verlinde gravity. Anyhow, we will cover the topics usually treated in the first semester of statistical mechanics.
As long as achieving our goals of understanding “loop quantum gravity,” “Verlinde gravity,” and “Cosmic Microwave Background anisotropies” are concerned, you must learn “general relativity” as it is the prerequisites to all these three subjects. Nevertheless, it is not usually a mandatory subject in college or graduate school. There are many subareas in physics in which the knowledge of general relativity is not required at all. General relativity, which is usually taught for senior physics major or first year physics graduate students, requires the knowledge of calculus, special relativity, and classical mechanics. Basic special relativity is usually taught in a freshman physics course, but advanced special relativity, which is required to understand general relativity, is taught in a classical mechanics course.
Anyhow, to study “loop quantum gravity,” you need to know “quantum mechanics” and “general relativity.” “Statistical mechanics” is also needed to understand the black hole thermodynamics, but at a very basic level. Therefore, I didn’t put an arrow from “statistical mechanics” to “loop quantum gravity” in the figure. To learn “Verlinde gravity,” you need to learn “general relativity,” but if you intend to learn it very superficially, i.e., at the level in which I derived the violation of equivalence principle from Verlinde gravity, you do not need to know it. All you need to know is “multivariable calculus” and some very basic ideas in “classical mechanics” and “electromagnetism.” To study CMB anisotropy, you need to know cosmology which requires both “statistical mechanics” and “general relativity.” Or, I should rather say, CMB anisotropy is a topic in cosmology.
If there are smaller goals than these three grand goals, that would be understanding “quantum mechanics” and “general relativity,” which revolutionized our understanding of nature. I am convinced that the epistemological views of philosophers who have no basic understanding of these two subjects can be possibly flawed. Even though these two subjects are prerequisites to loop quantum gravity, and there are many materials you need to learn before studying “loop quantum gravity” in these two subjects, I don’t confine myself to the strictly necessary prerequisites, as many topics in “quantum mechanics” and “general relativity” are interesting on their own. The same goes for prerequisites to “quantum mechanics,” “general relativity,” or any other subjects treated in my articles. If a topic is interesting enough, I explain, even though it is not a prerequisite to any other subjects treated in my articles.
After finishing writing most of the articles, I decided to add articles on the history of astronomy. Certainly, teaching physics, math, or astronomy by following the history of these subjects is not a good idea. For example, Sir Isaac Newton invented calculus and explained the motion of planets in his book “Principia.” However, it is a bad idea for modern readers to learn calculus or celestial mechanics by following “Principia.” In physics and math, there is something called a “modern perspective.” Some mathematical and scientific results which Newton derived in complicated ways can now be derived much more clearly and succinctly thanks to the work of mathematicians and physicists of the following generations after him. Also, these mathematicians and physicists found easier ways to explain things that Newton explained in a very complicated way. Then, why did I include the articles on the history of astronomy? Once you know the content, it is worth learning the history of how it was first discovered. You will appreciate how difficult it was to discover these things that we now take for granted too easily. I hear people saying that they would have discovered calculus if they were born in Newton’s time. They say so because calculus is very easy for them. But, don’t you know the famous story of “Columbus’ egg”? It’s much easier to understand a new discovery than to make the discovery by yourself. Anyhow, learning the history of astronomy will give you lessons which can be useful when you actually work as a scientist making discoveries and taking part in the new history.
At the end of every article, I included a summary, which you should remember. For some articles, I included exercises for the readers to solve. Some of them are intended for the readers to check whether they have grasped the key concepts in the article. Others are intended to give the readers the opportunities to derive the key concepts on their own, which are deliberately left out of the main article, as people remember better when they derive things on their own than when they just watch someone else derive them for them. I have tried to make such exercises as easy as necessary so that if the readers understand the key concepts, they are expected to solve such exercises correctly. Other exercises are intended to fill in the gaps between the reasoning. Of course, I could have presented the solutions in the main text instead of assigning exercises, but I wanted to give the readers some chances to think before checking the answers. I will upload the solutions later if I get a chance. As I give out hints for most exercises, make sure that you take some time trying to solve the exercises by yourself. Or, if you want to challenge yourself, you can try to solve them by yourself before consulting the hints.
The articles here explain high school mathematics, also known as “middle school mathematics” in South Korea. They also cover the Cauchy-Schwarz inequality, which is usually left out in a standard high school curriculum but is actually simple and interesting to learn.
The articles here can benefit everyone. Most require no specific knowledge, although some assume familiarity with high school mathematics. They can be understood both by laymen and by students learning high school physics.
The articles here are primarily targeted for mathematically oriented high school students and for students learning calculus. Science and engineering students can also benefit from some of these articles, especially the ones on quantum mechanics and on special relativity. Physics majors can also benefit from some of these articles, especially the ones on differential forms and on the Feynman diagram.
The articles here are suitable for advanced undergraduate physics majors and physics graduate students.
Sometimes, there are short-cut to interesting articles, if you are eager to reach them as soon as possible. See the figure below.
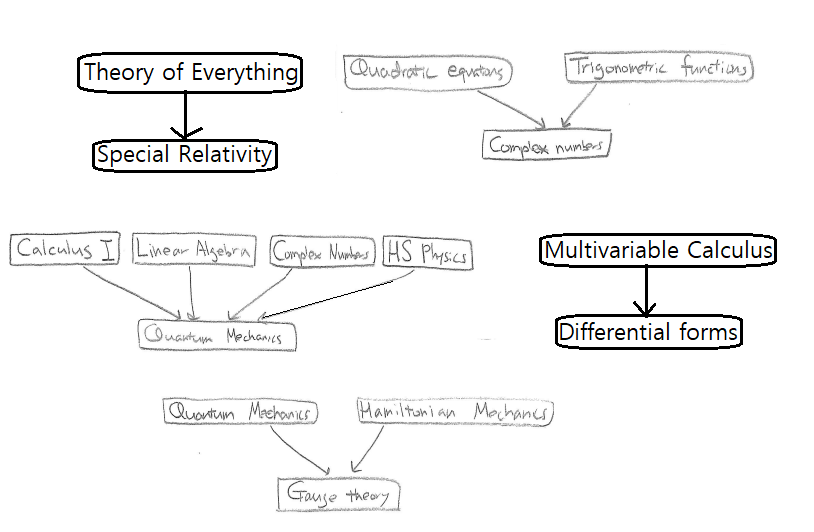
To see more of these, read the most recommended articles.