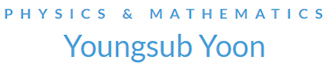Discrete area spectrum and the Hawking radiation spectrum II: Single unit area deduction
In the last article, I explained the reason why only discrete values of wavelengths of light must be emitted from black holes. There, I referred to the result of a paper by Bekenstein and Mukhanov in 1995: “The Hawking radiation allows only discrete value of wavelength if the area spectrum is discrete.”
However, in 1996, Barreira, Carfora and Rovelli argued that this was not the case. In other words, they argued that the spectrum of the Hawking radiation is continuous. Putting it differently again, they argued that the black hole emits all kinds of light as in the generic blackbody radiation.
Even though I read about this result from Quantum Gravity, a book written by Rovelli, I completely forgot about it. I did not know that the continuous Hawking spectrum was accepted in the loop quantum gravity community. So I used the discreteness of the Hawking radiation spectrum in my research in 2010, and obtained a positive result with it. Without it, there would have been no numerical agreement for a certain value obtained using two different methods. Later, when I read this part of the book again in 2011, I realized that an incorrect argument is presented in the book. Therefore, I wrote a very short paper showing that the Hawking radiation allows only discrete value of wavelength if the area spectrum is discrete, and sent my paper to Rovelli. After long discussions through emails, he acknowledged my idea and even gave me a hint to improve my argument. In this article, I explain, in laymen’s term, why Barreira, Carfora and Rovelli’s conclusion was wrong, and why my conclusion is correct.
To this end, let me briefly explain the spectroscopy of atoms. Under suitable conditions, an atom emits light with certain wavelengths which only depend on the kind of the atom. For example, the hydrogen atom emits light with certain wavelengths and the helium atom emits light with certain other wavelengths that differ from the hydrogen atom’s and so on.
In the late 19th century, Swedish physicist Rydberg found out that for a given kind of atom, the inverse of wavelength of the light emitted can be expressed as the difference of two arbitrarily chosen numbers from a set of numbers that only depend on the kind of atom. For example, if the set of numbers is following:
![]()
Then, the inverse of wavelengths emitted must be Ai-Aj, where i and j are natural numbers. In case of hydrogen, Ai is given by the following:
![]()
where R is called “Rydberg constant.” Therefore, λ, the wavelength of the light emitted from hydrogen, can be expressed as follows:
![]()
So, a natural question one may ask is “why can the inverse of wavelengths always be expressed as a difference of two terms?” The correct explanation came in 1913 from Niels Bohr. He argued that in an atom, the electrons move around only certain orbits, which in turn correspond to specific energies. When the electron changes its orbit, the energy of the atom changes by the difference between the energy of the atom before the emission and the energy of the atom after the emission. As energy is conserved, the atom emits light when the electron falls into an orbit with lower energy and the energy of the emitted light is given by this difference. As the atom can have only certain values of energy as its electrons have certain orbits, we conclude that the energy of emitted light is given by the difference of two terms, namely two possible energies an atom can have. As the energy of light is inversely proportional to wavelength, we conclude that the inverse of wavelength must be proportional to the difference of two energies an atom can have. Summarizing, we can conclude that the inverse of wavelength can be always expressed as a difference of two terms.
Now, let’s go back to black holes. When light is emitted from a black hole, the energy of the black hole decreases by the amount of the energy of light. In other words, the energy of light emitted from the black hole must be the difference between two energies a black hole can have.
In the case of the Bekenstein and Mukhanov’s scenario, the area of the black hole is an integer multiple of the certain unit area. As I explained in the earlier articles, this is not actually the case. There are many of unit areas. The Bekenstein/Mukhanov scenario is only a simplified model of the real situation. As the area of the black hole can only have discrete values, its energy can only have discrete values as well. Therefore, it is natural that the energy emitted from black hole can only have discrete values.
However, Barreira, Carfora and Rovelli argued that in the real situation a black hole can have almost continuous values for the area, and therefore for the energy as well. This is because there are infinite numbers of the unit area in reality, and summing them up we can get the spacing of the area spectrum to be very, very small.
Let me give you an example. If there is
only one unit area which is A, we can have A, 2A, 3A and so on for the area of
the black hole. We will never have the black hole area as a non-integer
multiple of A. The spacing of the area spectrum will be always A. However, if
the unit areas were A, 1.4A, 1.7A, 1.9A, 2.2A … we can
have A(=A), 1.4A(=1.4A), 1.7A(=1.7A), 1.9A(=1.9A), 2A(=A+A), 2.4A(=A+1.4A),
2.7A(=A+1.7A), 2.9A(=A+1.9A), 3A(A+A+A), 3.1A(=1.4A+1.7A), 3.2A(=A+2.2A),
3.3A(=1.4A+1.9A), 3.4A(=1.4A+A+A) and so on. Here, we see that we can have the
spacing of the area spectrum much less than A. For example, in the case of 3A
and 3.1A, the spacing is only 0.1A.
Actually, one can show that the spacing of the area spectrum quickly
becomes smaller and
smaller as the area concerned (in our case, the
black hole area) becomes bigger and bigger. This is actually the case because
the black hole area is much bigger than the unit area.
Therefore, Barreira, Carfora and Rovelli concluded that the energy of light emitted by a black hole must be almost continuous, as the energy a black hole can have is almost continuous and only the difference between two energy levels for the black hole can be the energy of light emitted.
Their argument that the black hole’s energy is almost continuous is correct, but the argument that the Hawking radiation spectrum is continuous is wrong. Where have they gone wrong?
They mistakenly thought that the area of the black hole after the emission of the single light can have any value allowed from the combination of unit areas as long as it is smaller than the original area. However, as I already pointed out in my previous article, the amount of the decrease of area must be an amount the area spectrum allows. To make it easier to understand, let’s return to our hypothetical example we considered. Barreira, Carfora and Rovelli thought that the black hole area can change from 3.2A(=A+2.2A) to 3.1A(=1.4A+1.7A) after the emission of single light. However this is not the case. It can only change to A or 2.2A. If it could change to 3.1A, it would imply that the whole geometry of the black hole can change to “1.4A+1.7A” in a single instant, which is nonsencial.
However, I was not sure whether the black
hole area could change from 3.4A(=1.4A+A+A) to 1.4A(=1.4A) or A(=A) instead of
2.4A(=1.4A+A) or 2A(=A+A). It could be possible because only part of the
geometry of the black hole changes, not the whole geometry. In other words, I
was not sure whether the black hole area could decrease by two or more area
units. (In case in which the area of the black hole changes from
3.4A(=1.4A+A+A) to 1.4A(=1.4A), the black hole area decreased by two area unit,
namely {A,A}. In case in which the area of the black hole changes from
3.4A(=1.4A+A+A) to A(=A), the black hole area decreased by two area unit,
namely {A, 1.4A}.) I suspected that it wouldn’t, from
my previous research, but I couldn’t see why it shouldn’t be from a more fundamental point of view. Nevertheless, I was sure
that Barreira, Carfora and Rovelli’s conclusion was not
correct. Without mentioning my uncertainty on the issue whether the black hole
area could decrease by two or more area units, I sent an email to Rovelli with
my paper attached, as I needed an “endorsement” to upload my paper on arXiv.org (a website where physicists upload
their papers.)
However, as my paper was quite poorly written, he didn’t initially understand my argument. He demanded more explanation so I explained it to him in more detail, which was pretty much the explanation that I gave earlier in this article. He finally understood, and also noted:
“On the substance, I am not yet fully convinced. Why should a photon (i.e. light particle) be emitted by a single puncture? For instance a process could merge two punctures into one, or split one into two, and so on. Maybe you have a principle of locality in mind, but, again, this should be said more precisely. Think! Take time!”
Not knowing what he meant by “locality,” I contacted a close of friend. I made an appointment to meet him the next day. Maybe, he could help me. So, I walked back to the dormitory to sleep. On the way home, I suddenly realized what he meant: A photon should be emitted from a single place, or a single “puncture;” it would be hard to imagine a single photon could be emitted from two or more places simultaneously.
Let me clarify this. See fig. 1.
In the figure, each “cell” or “puncture” has a unit area. If a photon is emitted from the area puncture as marked “I,” the area of black hole will decrease by the area of “I.” This is natural, and certainly possible.
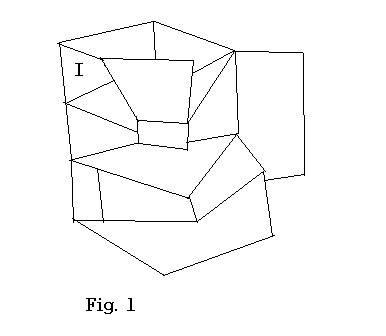
However, the case in which the area of the black hole decreases by two or more area units is troublesome. For example, if the black hole area decreases by two area units which are the area of “J” and the area of “K” as in Fig. 2, it would imply that a single photon is emitted from “J” and “K” simultaneously, which is certainly impossible.
I immediately canceled the appointment with
my friend. Later, I finished writing up my paper. Rovelli acknowledged it, and
provided me with an endorsement.
However, instead of allowing me to upload my paper, arXiv asked me whether I had “a conventional publication record.” I replied that I did not. Soon, they responded, “Your submissions have been removed upon a notice from our moderators, who determined them inappropriate for arXiv. Please send to a conventional journal instead for the requisite feedback.”
Therefore, I submitted it to a journal to get published. After two and half months, I heard back from them. The referee noted that I was not aware of an important paper related to my research. In the paper, Krasnov argued that the Hawking radiation spectrum is continuous (i.e. a black hole emits all kinds of light) as it would seem that a segment with a unit area can change into one with smaller unit area upon emission of light. He concluded this because the difference of two unit areas can be virtually any value according to loop quantum gravity, especially when there are an infinite number of them.
He used Hawking’s own Hawking radiation picture which is following: According to quantum mechanics, a pair of particles, one with positive energy and another with negative energy, can be created in a vacuum (i.e. out of nothing). This process is called “pair creation.” Hawking suggests that if pair creation takes place just outside of a black hole, the particle with negative energy (the ‘’negative’’ particle) will fall into the black hole, while the particle with positive energy (the ‘’positive” particle) will radiate away from the black hole. Thus, it will appear to us as though the positive particles were coming out of the black hole itself. At the same time, as the particles with negative energy fall into the black hole, the energy of the black hole will lessen, thus making the black hole smaller and smaller. Put another way, the black hole decreases in size as it loses matter.
Krasnov argued that a segment with a unit area changes into one with smaller unit area when the negative particle reaches that segment.
I pondered for a while, and walked back to the dormitory where I may have found some references to look at. On the way home, I came up with an idea that I thought was solution: It is well-known that an object falling into a black hole never reaches it, from the point of view of an observer outside the black hole. If one calculates the time it takes to reach the black hole, it is simply infinite, even though the object feels that it reaches the black hole in finite time. Therefore, one of the two pair-created photons supposed to reach the black hole and decrease the area of a single segment never does the job. So, I concluded, upon the emission of light, either the single segment disappears completely or it remains intact. Therefore, I thought I had successfully found an argument against the referee’s criticism.
With this result, I tried to publish my paper many times at different journals, but the referees never thought that my argument was convincing. I later learned, though not from the referees’ report, that Hawking argued the negative particle would be still able to reach the black hole by a process called “tunneling” which is a well-known phenomenon in quantum mechanics. According to quantum mechanics, you can “tunnel” and reach places that are classically forbidden. For example, you could conceivably reach into another room without opening the door through “tunneling” the door. Of course, the thicker the door, the smaller the probability that tunneling would take place. (However, Hawking never calculated the probability for a negative particle to tunnel into the inside of a black hole. Moreover, he described his picture of pair creation for particle creation by a black hole as follows: “It should be emphasized that these pictures of the mechanism responsible for the thermal emission and area decrease are heuristic only and should not be taken too literally….[]..The real justification of the thermal emission is the mathematical derivation given in Section {2}.”)
In spring 2015, I flipped through the famous quantum mechanics textbook by Griffiths, as I thought that it would be helpful in writing review articles for my homepage. There, I found out how the Bose-Einstein distribution, from which one can obtain Planck’s blackbody radiation by multiplying some factors, was derived in a novel way. As I was then looking for a way to rigorously derive a certain formula in a paper of mine with Brian Kong, I followed the derivation of Planck’s blackbody radiation in the book closely step by step. I didn’t succeeded in deriving the formula in my paper with Brian Kong then, but instead I suddenly found the step that implies that only a single unit area must be deducted from the area of black hole upon the emission of the light particle; the formula for the Hawking radiation spectrum, obtained using the method to derive the Bose-Einstein distribution in Griffiths’ book is valid only when an emitted light particle corresponds to a single unit area. Therefore, I wrote out and included my new idea into the new version of my paper and submitted to many journals one by one, but they all rejected it before Journal of the Korean Physical Society finally accepted it in spring 2016.
I will explain my idea in our later article “Quantum corrections to Hawking radiation spectrum.” Of course, to understand it, you would also need to know how the Bose-Einstein distribution is derived which is explained in the quantum mechanics textbook by Griffiths. This I will review in “The Bose-Einstein distribution, the Fermi-Dirac distribution and the Maxwell distribution.”