Expectation values in quantum field theory (2)

In my article "Expectation values in quantum field theory (1)," I gave you a basic idea of how physicists calculate the expectation values in quantum field theory. In this article, I provide additional details. This article assumes familiarity with multivariable calculus and linear algebra.

In the earlier article, I claimed the following:

 

You can learn how to derive this by checking out the following Wikipedia article:

http://en.wikipedia.org/wiki/Gaussian_integral#By_polar_coordinates

Also, the expectation value for  that I gave in the previous article is given generally by the following formula:

 

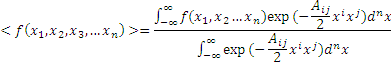
-1)

where we have used the Einstein summation convention.

To calculate this, we first observe the following formula:

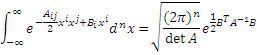
This formula is derived by generalizing the formula in the previous article. Now, as before, we can Taylor-expand  and obtain the relevant expectation values by differentiating the above formula with respect to s, and setting all s equal to zero.

For example, we have:

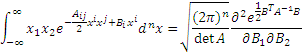
and we can set all s equal to zero at the end of the calculation.

So, you have learned how to calculate the expectation value for . However, in real physics, you may often find that the exponents in the formula for the expectation value are not simply quadratic in s, but also have higher order terms. However, this should be no problem, as you can Taylor-expand the exponents and obtain another polynomial while making the exponents quadratic in s. For example, if we have a cubic term in the exponent, we have:

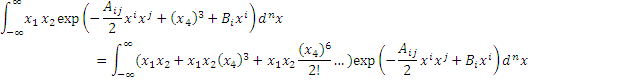
Each term in this expansion can be calculated by differentiating with respect to s as explained previously. Also, each term can be represented by a diagram called the “Feynman diagram” the details of which are the topic of the following article.